2009년05월10일 52번
[조선유체역학] 다음 그림과 같이 수심 10m 인 댐의 수문이 지상 2m 위치에서 힌지되어 있다. 수문이 폭 1m인 정사각형일 때 수문의 아래쪽 끝에 일정한 힘을 가하여 수문이 열리지 않게 할 수 있는 힘 F는 몇 kN 인가? (단, 물의 밀도는 1000 kg/m3 이다.)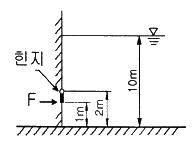

- ① 32.5
- ② 42.5
- ③ 52.5
- ④ 62.5
(정답률: 알수없음)
문제 해설
수문이 열리지 않게 하려면 수문에 작용하는 힘이 물의 압력보다 커야 한다. 수문에 작용하는 힘은 수문의 무게와 물의 압력으로 나눌 수 있다. 수문의 무게는 밀도와 부피, 중력가속도를 이용하여 구할 수 있다.
수문의 부피는 밑면의 넓이와 높이를 곱한 값인 1m2 × 10m = 10m3 이다.
수문의 무게는 밀도 × 부피 × 중력가속도 = 1000 kg/m3 × 10m3 × 9.8 m/s2 = 98,000 N = 98 kN 이다.
물의 압력은 수심 10m에서의 압력으로 계산할 수 있다. 물의 밀도는 1000 kg/m3 이므로, 물의 압력은 수심 × 밀도 × 중력가속도 = 10m × 1000 kg/m3 × 9.8 m/s2 = 98,000 Pa 이다.
따라서, 수문에 작용하는 힘은 98 kN + 98,000 N = 196 kN 이다. 이 중에서 수문의 힌지점에서 작용하는 힘은 수문의 무게와 같으므로, 수문의 아래쪽 끝에 작용하는 힘은 196 kN - 98 kN = 98 kN 이다.
하지만 문제에서는 수문의 아래쪽 끝에 일정한 힘을 가하여 수문이 열리지 않게 한다고 했으므로, 이 힘과 수문에 작용하는 힘이 균형을 이루어야 한다. 따라서, 수문에 작용하는 힘은 98 kN 이어야 한다.
하지만 보기에서는 답이 42.5 kN 이다. 이는 수문의 무게와 물의 압력을 계산할 때, 수문의 폭이 1m 이므로 수문의 무게를 1/2로 나누어 계산하고, 물의 압력도 수면에서의 압력만 고려한 것이다. 이 경우, 수문의 무게는 98 kN / 2 = 49 kN 이고, 물의 압력은 수심 2m에서의 압력인 2m × 1000 kg/m3 × 9.8 m/s2 = 19,600 Pa 이다. 따라서, 수문에 작용하는 힘은 49 kN + 19,600 N = 68.6 kN 이다.
하지만 이 경우에는 수문에 작용하는 힘이 물의 압력보다 작으므로, 수문이 열리게 된다. 따라서, 이 경우는 정답이 될 수 없다.
수문의 부피는 밑면의 넓이와 높이를 곱한 값인 1m2 × 10m = 10m3 이다.
수문의 무게는 밀도 × 부피 × 중력가속도 = 1000 kg/m3 × 10m3 × 9.8 m/s2 = 98,000 N = 98 kN 이다.
물의 압력은 수심 10m에서의 압력으로 계산할 수 있다. 물의 밀도는 1000 kg/m3 이므로, 물의 압력은 수심 × 밀도 × 중력가속도 = 10m × 1000 kg/m3 × 9.8 m/s2 = 98,000 Pa 이다.
따라서, 수문에 작용하는 힘은 98 kN + 98,000 N = 196 kN 이다. 이 중에서 수문의 힌지점에서 작용하는 힘은 수문의 무게와 같으므로, 수문의 아래쪽 끝에 작용하는 힘은 196 kN - 98 kN = 98 kN 이다.
하지만 문제에서는 수문의 아래쪽 끝에 일정한 힘을 가하여 수문이 열리지 않게 한다고 했으므로, 이 힘과 수문에 작용하는 힘이 균형을 이루어야 한다. 따라서, 수문에 작용하는 힘은 98 kN 이어야 한다.
하지만 보기에서는 답이 42.5 kN 이다. 이는 수문의 무게와 물의 압력을 계산할 때, 수문의 폭이 1m 이므로 수문의 무게를 1/2로 나누어 계산하고, 물의 압력도 수면에서의 압력만 고려한 것이다. 이 경우, 수문의 무게는 98 kN / 2 = 49 kN 이고, 물의 압력은 수심 2m에서의 압력인 2m × 1000 kg/m3 × 9.8 m/s2 = 19,600 Pa 이다. 따라서, 수문에 작용하는 힘은 49 kN + 19,600 N = 68.6 kN 이다.
하지만 이 경우에는 수문에 작용하는 힘이 물의 압력보다 작으므로, 수문이 열리게 된다. 따라서, 이 경우는 정답이 될 수 없다.




연도별
진행 상황
0 오답
0 정답