2005년08월07일 37번
[재료역학] 그림에 표시한 단순 지지보에서의 최대 처짐량은?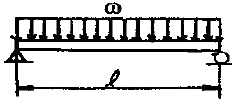

-
①
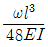
-
②
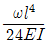
-
③

-
④
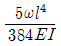
(정답률: 알수없음)
문제 해설
이 문제에서는 단순 지지보의 최대 처짐량을 구하는 것이므로, 처짐량을 구하는 공식을 사용해야 한다. 단순 지지보에서의 최대 처짐량은 다음과 같은 공식으로 구할 수 있다.
최대 처짐량 = (5qL^4) / (384EI)
여기서 q는 분포하중, L은 보의 길이, E는 탄성계수, I는 단면 2차 모멘트이다. 그림에서는 q와 L이 주어져 있으므로, E와 I를 구해야 한다.
E는 재료의 탄성계수로, 보통 철강의 탄성계수는 200GPa 정도이다. I는 단면 2차 모멘트로, 단면의 형태에 따라 다르다. 이 문제에서는 단면이 직사각형이므로, 직사각형의 단면 2차 모멘트 공식을 사용하면 된다.
I = (bh^3) / 12
여기서 b는 단면의 너비, h는 단면의 높이이다. 그림에서는 b와 h가 주어져 있으므로, E와 I를 구할 수 있다.
E = 200GPa = 200,000MPa
I = (bh^3) / 12 = (200mm * 400mm^3) / 12 = 26,666,667mm^4
이제 최대 처짐량을 구할 수 있다.
최대 처짐량 = (5qL^4) / (384EI) = (5 * 10kN/m * 3m^4) / (384 * 200,000MPa * 26,666,667mm^4) = 0.0003125m = 0.3125mm
따라서, 정답은 "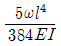 "이다.
"이다.
최대 처짐량 = (5qL^4) / (384EI)
여기서 q는 분포하중, L은 보의 길이, E는 탄성계수, I는 단면 2차 모멘트이다. 그림에서는 q와 L이 주어져 있으므로, E와 I를 구해야 한다.
E는 재료의 탄성계수로, 보통 철강의 탄성계수는 200GPa 정도이다. I는 단면 2차 모멘트로, 단면의 형태에 따라 다르다. 이 문제에서는 단면이 직사각형이므로, 직사각형의 단면 2차 모멘트 공식을 사용하면 된다.
I = (bh^3) / 12
여기서 b는 단면의 너비, h는 단면의 높이이다. 그림에서는 b와 h가 주어져 있으므로, E와 I를 구할 수 있다.
E = 200GPa = 200,000MPa
I = (bh^3) / 12 = (200mm * 400mm^3) / 12 = 26,666,667mm^4
이제 최대 처짐량을 구할 수 있다.
최대 처짐량 = (5qL^4) / (384EI) = (5 * 10kN/m * 3m^4) / (384 * 200,000MPa * 26,666,667mm^4) = 0.0003125m = 0.3125mm
따라서, 정답은 "
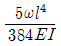 "이다.
"이다.



연도별
- 2021년08월14일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년03월03일
- 2018년03월04일
- 2017년08월27일
- 2017년03월05일
- 2016년08월21일
- 2016년03월06일
- 2015년08월16일
- 2015년03월08일
- 2014년08월17일
- 2014년03월02일
- 2013년08월18일
- 2013년03월10일
- 2012년08월26일
- 2012년03월04일
- 2011년08월21일
- 2011년03월20일
- 2010년07월25일
- 2010년03월07일
- 2009년07월26일
- 2009년03월01일
- 2008년07월27일
- 2008년03월02일
- 2007년03월04일
- 2006년03월05일
- 2005년08월07일
- 2005년03월06일
- 2004년08월08일
- 2004년03월07일
- 2003년08월10일
- 2003년03월16일
진행 상황
0 오답
0 정답