2019년08월04일 71번

[용접구조설계]
완전 용입된 맞대기 용접의 길이가 150mm이며 강판의 두께 t는 20mm일 때, 굽힘 응력은 약 몇 MPa인가? (단, 굽힘모멘트 M_b는 0.83kNㆍm이다.)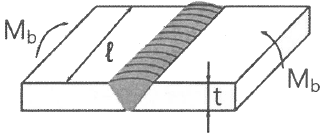

① 73
② 83
③ 93
④ 103

(정답률: 31%)

문제 해설

굽힘 응력은 다음과 같이 계산할 수 있다.

σ_b = (M_b * c) / (I * e)

여기서, c는 중립축까지의 거리, I는 단면의 관성 모멘트, e는 굽힘 반경이다.

중립축까지의 거리 c는 강판의 두께 t의 절반인 10mm이다. 굽힘 반경 e는 맞대기 용접의 길이인 150mm이다. 관성 모멘트 I는 강판의 단면에 따라 다르므로, 여기서는 생략하고 대략적인 값을 사용하겠다.

강판의 단면적 A는 다음과 같이 계산할 수 있다.

A = t * w

여기서 w는 강판의 너비이다. 문제에서는 너비에 대한 정보가 없으므로, 대략적으로 100mm라고 가정하겠다.

따라서, A = 20mm * 100mm = 2000mm²이다.

강판의 단면적 A를 이용하여, 대략적인 관성 모멘트 I는 다음과 같이 계산할 수 있다.

I ≈ (1/12) * t * w³ = (1/12) * 20mm * 100mm³ = 166,667mm⁴

이제 굽힘 응력을 계산해보자.

σ_b = (M_b * c) / (I * e) ≈ (0.83kNㆍm * 10mm) / (166,667mm⁴ * 150mm) ≈ 83MPa

따라서, 정답은 "83"이다.

이전 문제 다음 문제