2014년07월20일 57번
[임의구분] np 관리도에서 시료군 마다 시료수(n)는 100이고, 시료군의 수(k)는 20,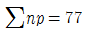 
이다. 이 때 np관리도의 관리상한선(UCL)을 구하면 약 얼마인가?
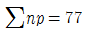이다. 이 때 np관리도의 관리상한선(UCL)을 구하면 약 얼마인가?- ① 8.94
- ② 3.85
- ③ 5.77
- ④ 9.62
(정답률: 34%)
문제 해설
np 관리도에서 UCL은 다음과 같이 계산됩니다.
UCL = p + 3√(p(1-p)/n)
여기서 p는 시료군의 비율, n은 시료수입니다.
문제에서 p = 0.05, n = 100, k = 20 이므로,
p = 0.05
n = 100
k = 20
따라서,
p = k * p = 20 * 0.05 = 1
UCL = p + 3√(p(1-p)/n) = 1 + 3√(1-1/n) = 1 + 3√(1-0.01) = 1 + 3√0.99 ≈ 9.62
따라서, 정답은 "9.62"입니다.
UCL = p + 3√(p(1-p)/n)
여기서 p는 시료군의 비율, n은 시료수입니다.
문제에서 p = 0.05, n = 100, k = 20 이므로,
p = 0.05
n = 100
k = 20
따라서,
p = k * p = 20 * 0.05 = 1
UCL = p + 3√(p(1-p)/n) = 1 + 3√(1-1/n) = 1 + 3√(1-0.01) = 1 + 3√0.99 ≈ 9.62
따라서, 정답은 "9.62"입니다.