화약류관리기사 기출문제·모의고사·오답노트·자동채점
App Store에서 다운로드 APK 다운로드
연도별 풀이 오답노트 별표문제
  1. 홈
    2. ›
  2. 화약류관리기사
    3. ›
  3. 2011년03월20일
    4. ›
  4. 47번

2011년03월20일 47번

[암석역학]
다음 그림과 같이 경사면 상부에 암석 블록이 놓여있을 때, 점착력을 무시하고 마찰력에 의해서만 블록이 지지된다고 가정하면 이 암석 블록이 안정하기 위한 조건은 무엇인가? (단, 암석 블록의 높이와 폭은 각각 h, b이고, 블록저면과 사면의 마찰각은 ø, 그리고 사면 경사각은 Ψ이다.)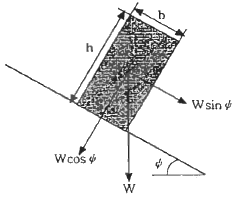

  • ① Ψ＜ø, b/h＜tanΨ
  • ② Ψ＜ø. b/h＞tanΨ
  • ③ Ψ＞ø. b/h＜tanΨ
  • ④ Ψ＞ø. b/h＞tanΨ
(정답률: 30%)

문제 해설

암석 블록이 안정하기 위해서는 블록이 미끄러지지 않도록 마찰력이 중력과 같거나 크게 작용해야 한다. 이를 수식으로 나타내면 다음과 같다.

μN ≥ mg

여기서 μ는 마찰계수, N은 블록에 작용하는 수직력, m은 블록의 질량, g는 중력가속도이다. 수직력 N은 블록의 무게와 수직 방향의 압력으로 인해 다음과 같이 구할 수 있다.

N = mg cosΨ

여기서 Ψ는 사면 경사각이다. 따라서 마찰력이 중력과 같거나 크게 작용하기 위한 조건은 다음과 같다.

μmg cosΨ ≥ mg

이를 정리하면 다음과 같다.

μ ≥ 1/cosΨ

여기서 cosΨ는 1보다 작으므로 마찰계수는 1보다 커야 한다. 따라서 마찰각 ø보다 사면 경사각 Ψ가 작아야 한다.

또한, 블록이 미끄러지지 않도록 하기 위해서는 블록의 무게가 수직 방향으로 작용하는 힘보다 크게 작용해야 한다. 이를 수식으로 나타내면 다음과 같다.

μN sinΨ ≥ mg sinθ

여기서 θ는 블록이 미끄러질 때의 경사각이다. 이를 정리하면 다음과 같다.

μmg cosΨ sinΨ ≥ mg sinθ

cosΨ와 sinΨ는 서로 대응되는 삼각함수이므로 다음과 같이 변형할 수 있다.

μmg sinΨ/cosΨ ≥ mg sinθ

여기서 sinθ는 블록이 미끄러질 때의 경사각이므로 tanθ = b/h이다. 따라서 위 식은 다음과 같이 정리할 수 있다.

μmg tanΨ ≥ mg b/h

양변을 m과 g로 나누면 다음과 같다.

μtanΨ ≥ b/h

따라서 블록이 미끄러지지 않도록 하기 위한 조건은 마찰각 ø보다 사면 경사각 Ψ가 작아야 하고, b/h는 tanΨ보다 커야 한다. 이를 종합하면 "Ψ＜ø. b/h＞tanΨ"가 된다.
이전 문제 다음 문제
AppStore에서 다운로드 APK 다운로드

연도별

진행 상황

0 오답
0 정답