2002년05월26일 13번

[기계가공법 및 안전관리]
그림과 같이 양단이 고정된 균일 단면봉에서 중간 m-n 단면의 중간점에 축하중 P 가 작용할 때 양단의 반력 R₁과 R₂는 각각 몇 N인가? (단, P = 1 kN 이다.)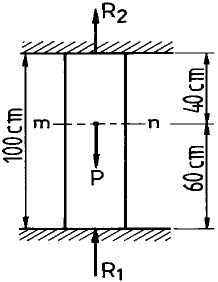

① R1=0.6, R2=0.4
② R1=0.4, R2=0.6
③ R1=0.75, R2=0.25
④ R1=0.25, R2=0.75

(정답률: 39%)

문제 해설

이 문제는 정적 평형을 이용하여 풀 수 있다. 중간 m-n 단면을 기준으로 왼쪽과 오른쪽으로 나누어 각각의 정적 평형을 구해보자.

왼쪽 부분의 정적 평형을 구해보면, P와 R₁이 y축 방향으로 작용하고 있으므로 x축 방향으로의 합력은 0이다. 따라서 R₂는 P와 R₁의 합력과 같은 크기를 가지고 반대 방향으로 작용해야 한다. 이를 수식으로 나타내면 다음과 같다.

R₂ = P + R₁ = 1 kN + R₁

오른쪽 부분의 정적 평형을 구해보면, P와 R₂가 y축 방향으로 작용하고 있으므로 x축 방향으로의 합력은 0이다. 따라서 R₁은 P와 R₂의 합력과 같은 크기를 가지고 반대 방향으로 작용해야 한다. 이를 수식으로 나타내면 다음과 같다.

R₁ = P + R₂ = 1 kN + R₂

따라서 위의 두 식을 연립하여 R₁과 R₂를 구할 수 있다.

R₁ = 0.4 kN
R₂ = 0.6 kN

따라서 정답은 "R₁=0.4, R₂=0.6"이다.

이전 문제 다음 문제