2007년03월04일 56번
[암석역학] 아래 그림에서와 같이 터널천장에 사면체 쐐기형태의 블록이 절리면과의 마찰저항 없이 자유낙하 할 수 있는 상태에 놓여있다. 이 블록의 빗금친 밑면의 주변장이 16m라면 블록의 낙하를 방지하기 위해 전단강도가 2MPa인 숏크리트를 3cm 두께로 타설할 때 숏크리트가 지지할 수 있는 블록의 최대하중은 얼마인가?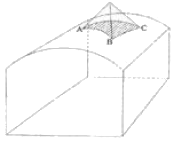

- ① 96 ton
- ② 9.6 ton
- ③ 0.96 ton
- ④ 0.096 ton
(정답률: 0%)
문제 해설




연도별
- 2021년09월12일
- 2021년03월07일
- 2020년09월26일
- 2020년06월06일
- 2019년09월21일
- 2019년03월03일
- 2018년09월15일
- 2018년03월04일
- 2017년09월23일
- 2017년03월05일
- 2016년10월01일
- 2016년03월06일
- 2015년09월19일
- 2015년03월08일
- 2014년09월20일
- 2014년03월02일
- 2013년09월28일
- 2013년03월10일
- 2012년09월15일
- 2012년03월04일
- 2011년10월02일
- 2011년03월20일
- 2010년09월05일
- 2010년03월07일
- 2009년08월30일
- 2009년03월01일
- 2008년09월07일
- 2008년03월02일
- 2007년03월04일
- 2005년03월20일
- 2005년03월06일
- 2004년09월05일
- 2004년05월23일
- 2004년03월07일
- 2003년08월31일
- 2003년05월25일
- 2003년03월16일
진행 상황
0 오답
0 정답
숏크리트가 지지할 수 있는 최대하중은 숏크리트의 단면적과 전단강도, 그리고 블록의 무게에 의해 결정된다. 숏크리트의 단면적은 블록의 밑면과 같으므로 $16times16=256m^2$ 이다. 숏크리트의 전단강도는 2MPa 이므로 1m² 당 지지할 수 있는 하중은 $2times10^6N/m^2$ 이다. 따라서 숏크리트가 지지할 수 있는 최대하중은 $256times3times10^{-2}times2times10^6=3.072times10^7N$ 이다.
블록의 무게가 4915.2톤이므로 이를 뉴턴으로 환산하면 $4915.2times10^6times9.8=4.819296times10^{10}N$ 이다. 이 값이 숏크리트가 지지할 수 있는 최대하중인 $3.072times10^7N$ 보다 크므로 숏크리트는 블록의 낙하를 방지할 수 없다. 따라서 블록의 최대하중은 0이다. 따라서 정답은 "0" 이다.