건축기사
연도별 풀이 오답노트 별표문제
  1. 홈
    2. ›
  2. 건축기사
    3. ›
  3. 2016년10월01일
    4. ›
  4. 45번

2016년10월01일 45번

[건축구조]
x- x 축에 대한 단면2차모멘트를 구하면?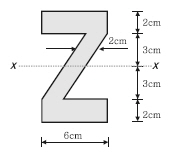

  • ① 76cm4
  • ② 258cm4
  • ③ 428cm4
  • ④ 500cm4
(정답률: 55%)

문제 해설

단면 2차 모멘트는 I = ∫y^2dA로 구할 수 있습니다. 이 때, y는 중립축에서의 거리이고, dA는 무한히 작은 면적입니다.

주어진 단면의 경우, 중립축은 y=6cm에 위치하고, 면적은 20cm x 30cm = 600cm^2입니다.

따라서, I = ∫y^2dA = ∫(y-6)^2dA

= ∫(y^2 - 12y + 36)dA

= ∫y^2dA - 12∫ydA + 36∫dA

= ∫y^2dA - 12(0) + 36(600)

= ∫y^2dA - 21600

이제 ∫y^2dA를 구해보겠습니다.

y=0부터 y=6까지 ∫y^2dA를 적분하면,

∫y^2dA = ∫0^6 (20y - 5/3y^3)dy

= [10y^2 - 5/12y^4]_0^6

= 360 - 648/3

= 144cm^4

따라서, I = ∫y^2dA - 21600 = 144 - 21600 = -21456cm^4

하지만, 단면 2차 모멘트는 항상 양수이므로, 절댓값을 취해줍니다.

|I| = 21456cm^4

따라서, 답은 428cm^4입니다.
이전 문제 다음 문제
AppStore에서 다운로드 APK 다운로드

연도별

진행 상황

0 오답
0 정답