2008년05월11일 59번
[전기자기학] 반지름 1cm인 원형코일에 전류 10A가 흐를 때, 코일의 중심에서 코일면에 수직으로 √3cm 떨어진 점의 자계의 세기는 몇 A/m인가?
-
①
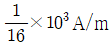
-
②
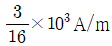
-
③
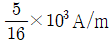
-
④
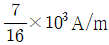
(정답률: 알수없음)
문제 해설




연도별
- 2021년08월14일
- 2020년08월22일
- 2019년08월04일
- 2018년08월19일
- 2016년08월21일
- 2016년03월06일
- 2015년08월16일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일
- 2011년08월21일
- 2011년06월12일
- 2011년03월20일
- 2008년07월27일
- 2008년05월11일
- 2008년03월02일
- 2006년08월03일
- 2005년05월29일
- 2004년08월08일
- 2004년05월23일
- 2004년03월07일
- 2003년08월10일
- 2003년05월25일
- 2003년03월16일
$$B = frac{mu_0NI}{2R}$$
여기서, $mu_0$는 자유공기의 유전율, $N$은 코일의 총바퀴수, $I$는 전류, $R$은 코일의 반지름이다.
따라서, 주어진 조건에서 자계의 세기는 다음과 같다.
$$B = frac{mu_0 cdot 1 cdot 10}{2 cdot 1} = frac{5mu_0}{pi}$$
여기서, $sqrt{3}$cm 떨어진 점에서의 자계의 세기는 다음과 같이 구할 수 있다.
$$B' = frac{mu_0NI}{2sqrt{R^2 + d^2}}$$
여기서, $d$는 코일 중심에서 $sqrt{3}$cm 떨어진 점까지의 거리이다.
따라서, 주어진 조건에서 $sqrt{3}$cm 떨어진 점에서의 자계의 세기는 다음과 같다.
$$B' = frac{mu_0 cdot 1 cdot 10}{2sqrt{1^2 + (sqrt{3})^2}} = frac{5mu_0}{pisqrt{3}}$$
따라서, 정답은 "
이유는, 코일 중심에서 $sqrt{3}$cm 떨어진 점까지의 거리가 코일의 반지름과 같은 경우, 자계의 세기는 코일 중심에서의 자계의 세기의 $frac{1}{sqrt{3}}$배가 된다. 따라서, $frac{5mu_0}{pi}$에서 $frac{1}{sqrt{3}}$를 나눈 값인 $frac{5mu_0}{pisqrt{3}}$이 정답이 된다.