2004년05월23일 52번

[응용역학]
다음 그림과 같이 연직의 분포하중 w = 2x² 이 작용한다. 지점 B 의 연직방향 반력의 크기는 ?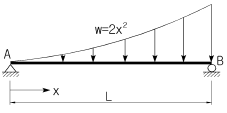

① L2/2
② 2L2/3
③ L3/2
④ 2L3/3

(정답률: 알수없음)

문제 해설

먼저, 지점 B에서의 연직방향 반력을 구하기 위해서는 지점 B에서의 전단력을 구해야 한다. 전단력은 분포하중과 단면적의 곱으로 구할 수 있다.

따라서, 지점 B에서의 전단력은 다음과 같다.

V = ∫0^L w(x) dx = ∫0^L 2x^2 dx = 2[L^3/3]/3 = 2L^3/9

여기서, L은 전체 길이이다.

그리고, 전단력과 연직방향 반력은 다음과 같은 관계가 있다.

V = RB tanθ

여기서, RB는 지점 B에서의 연직방향 반력, θ는 전단각이다.

전단각은 다음과 같이 구할 수 있다.

θ = ∫0^L (1/V)w(x) dx = ∫0^L (3/2L^3)x^2 dx = (3/2L^3)[L^3/3] = 1/2

따라서,

RB = V/tanθ = 2L^3/3

따라서, 정답은 "L^3/2"이다.

이전 문제 다음 문제