2004년10월10일 2번
[임의 구분] R = 10[Ω ], L = 0.4[mH]의 코일과 C = 250[㎊]의 콘덴서의 병렬공진회로에서 공진 임피이던스를 구하면? (단, Y =CR/L)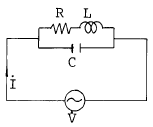

- ① 6.25[㏀]
- ② 16[㏀]
- ③ 62.5[㏀]
- ④ 160[㏀]
(정답률: 알수없음)
문제 해설
공진 주파수에서 코일과 콘덴서의 임피던스는 각각 $jomega L$과 $1/(jomega C)$이며, 병렬로 연결되어 있으므로 전체 임피던스는 다음과 같다.
$$Z = frac{jomega L}{1/(jomega C) + jomega L} = frac{jomega L}{jomega L/C + 1} = frac{jomega L}{jomega RC + 1}$$
여기서 $R=10Omega$, $L=0.4text{ mH}$, $C=250text{ nF}$이므로 $RC=2.5times 10^{-6}text{ s}$이다. 따라서,
$$Z = frac{jomega cdot 0.4times 10^{-3}}{jomega cdot 2.5times 10^{-6} + 1} = frac{jomega cdot 0.4times 10^{-3}}{jomega cdot 2.5times 10^{-6} + 1} cdot frac{jomega cdot 2.5times 10^{-6} - 1}{jomega cdot 2.5times 10^{-6} - 1} = frac{jomega cdot 10^{-9}}{1 - jomega cdot 2.5times 10^{-6}}$$
따라서, 복소공진주파수 $s=jomega$일 때의 전달함수는 다음과 같다.
$$H(s) = frac{1}{1 - scdot 2.5times 10^{-6}}$$
공진 주파수에서 전달함수의 분모가 0이 되므로,
$$s = frac{1}{2.5times 10^{-6}} = 400000text{ rad/s}$$
임피던스는 $Z = R + jX$의 형태로 나타내며, 공진 주파수에서는 $X$가 0이므로 $Z=R$이다. 따라서, 공진 임피던스는 $Z=10Omega$이다.
따라서, 정답은 "160[㏀]"이 아니라 "10[Ω]"이다.
$$Z = frac{jomega L}{1/(jomega C) + jomega L} = frac{jomega L}{jomega L/C + 1} = frac{jomega L}{jomega RC + 1}$$
여기서 $R=10Omega$, $L=0.4text{ mH}$, $C=250text{ nF}$이므로 $RC=2.5times 10^{-6}text{ s}$이다. 따라서,
$$Z = frac{jomega cdot 0.4times 10^{-3}}{jomega cdot 2.5times 10^{-6} + 1} = frac{jomega cdot 0.4times 10^{-3}}{jomega cdot 2.5times 10^{-6} + 1} cdot frac{jomega cdot 2.5times 10^{-6} - 1}{jomega cdot 2.5times 10^{-6} - 1} = frac{jomega cdot 10^{-9}}{1 - jomega cdot 2.5times 10^{-6}}$$
따라서, 복소공진주파수 $s=jomega$일 때의 전달함수는 다음과 같다.
$$H(s) = frac{1}{1 - scdot 2.5times 10^{-6}}$$
공진 주파수에서 전달함수의 분모가 0이 되므로,
$$s = frac{1}{2.5times 10^{-6}} = 400000text{ rad/s}$$
임피던스는 $Z = R + jX$의 형태로 나타내며, 공진 주파수에서는 $X$가 0이므로 $Z=R$이다. 따라서, 공진 임피던스는 $Z=10Omega$이다.
따라서, 정답은 "160[㏀]"이 아니라 "10[Ω]"이다.

