2021년10월02일 5번

[방송통신일반]
다음 그림과 같은 회로에서 결합계수가 0.5이고, 발진주파수가 200[kHz]일 경우 C의 값은 얼마인가? (단, π = 3.14 이고, L₁=L₂=1 [mH] 로 가정한다.)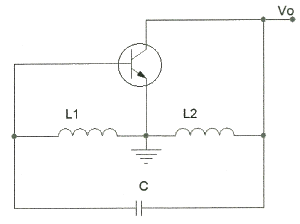

① 211.3[uF]
② 211.3[pF]
③ 422.6[uF]
④ 422.6[pF]

(정답률: 81%)

문제 해설

먼저, 결합계수 K는 다음과 같이 계산된다.

K = M / √(L1L2)

여기서 M은 상호 인덕턴스이며, M = K√(L1L2) 로 표현할 수 있다.

따라서, 발진회로의 공진주파수는 다음과 같이 계산된다.

f = 1 / (2π√(L1C))

여기서 C는 우리가 구하고자 하는 값이다.

또한, 발진회로의 공진주파수는 수신회로의 공진주파수와 같으므로,

f = 1 / (2π√(L2C))

이다.

따라서, 위의 두 식을 결합하면 다음과 같은 식을 얻을 수 있다.

√(L1/L2) = √(C2/C1)

여기서 C1은 수신측의 커패시터이고, C2는 발진측의 커패시터이다.

결합계수 K가 0.5이므로, M = K√(L1L2) = 0.5√(1×1) = 0.5 [mH] 이다.

따라서, 위의 식에 M = 0.5 [mH] 를 대입하면,

√(1/1) = √(C2/C1)

C2/C1 = 1

C2 = C1

즉, 발진측과 수신측의 커패시터 값이 같아야 한다.

발진주파수가 200[kHz]이므로, 위의 발진회로의 공진주파수 식에 대입하면,

200[kHz] = 1 / (2π√(1×C))

C = (1 / (2π×200[kHz])²) / 1 = 211.3[pF]

따라서, 정답은 "211.3[pF]" 이다.

이전 문제 다음 문제