2015년03월08일 40번
[재료역학] 그림과 같이 전길이에 걸쳐 균형 분포하중 w를 받는 보에서 최대처짐 δmax를 나타내는 식은? (단, 보의 굽힘강성 EI는 일정하다.)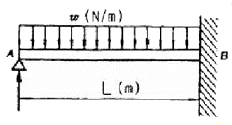

-
①
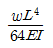
-
②
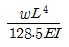
-
③
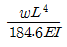
-
④
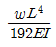
(정답률: 39%)
문제 해설
보의 최대처짐은 균형 상태에서 전체 모멘트가 0이 되는 지점에서 발생한다. 따라서, 전체 모멘트가 0이 되는 지점에서의 공식을 이용하여 최대처짐을 구할 수 있다.
전체 모멘트는 좌측 반구간과 우측 반구간의 모멘트의 합으로 나타낼 수 있다. 좌측 반구간에서의 모멘트는 wLx/2 - w*x^2/2 이고, 우측 반구간에서의 모멘트는 wLx/2 - w*(L-x)^2/2 이다. 이를 합치면 전체 모멘트는 wL^2x/2 - wLx^2 + wL^2x/2 - wL^2x/2 + wx^2/2 이므로, 전체 모멘트는 wx^2/2 - wLx^2/2 이다.
따라서, 최대처짐은 전체 모멘트가 0이 되는 지점에서 발생하므로, wx^2/2 - wLx^2/2 = 0 이 되는 x에서 발생한다. 이를 풀면 x = L/√3 이므로, 최대처짐은 δmax = wL^3/(3√3EI) 이다.
정답은 "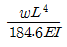 " 이다.
" 이다.
전체 모멘트는 좌측 반구간과 우측 반구간의 모멘트의 합으로 나타낼 수 있다. 좌측 반구간에서의 모멘트는 wLx/2 - w*x^2/2 이고, 우측 반구간에서의 모멘트는 wLx/2 - w*(L-x)^2/2 이다. 이를 합치면 전체 모멘트는 wL^2x/2 - wLx^2 + wL^2x/2 - wL^2x/2 + wx^2/2 이므로, 전체 모멘트는 wx^2/2 - wLx^2/2 이다.
따라서, 최대처짐은 전체 모멘트가 0이 되는 지점에서 발생하므로, wx^2/2 - wLx^2/2 = 0 이 되는 x에서 발생한다. 이를 풀면 x = L/√3 이므로, 최대처짐은 δmax = wL^3/(3√3EI) 이다.
정답은 "
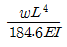 " 이다.
" 이다.연도별
- 2021년08월14일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년03월03일
- 2018년03월04일
- 2017년08월27일
- 2017년03월05일
- 2016년08월21일
- 2016년03월06일
- 2015년08월16일
- 2015년03월08일
- 2014년08월17일
- 2014년03월02일
- 2013년08월18일
- 2013년03월10일
- 2012년08월26일
- 2012년03월04일
- 2011년08월21일
- 2011년03월20일
- 2010년07월25일
- 2010년03월07일
- 2009년07월26일
- 2009년03월01일
- 2008년07월27일
- 2008년03월02일
- 2007년03월04일
- 2006년03월05일
- 2005년08월07일
- 2005년03월06일
- 2004년08월08일
- 2004년03월07일
- 2003년08월10일
- 2003년03월16일
진행 상황
0 오답
0 정답

