2015년05월31일 15번
[일반기계공학] 지름이 4mm인 강선이 그림과 같이 반지름이 500mm인 원통 위에서 휘어져 있을 때 최대굽힘 응력은 몇 kgf/cm2 인가? (단, E=2.0×106kgf/cm2 이다)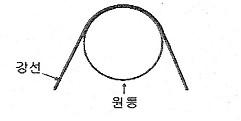

- ① 796.8
- ② 1593.6
- ③ 7968
- ④ 15936
(정답률: 44%)
문제 해설
최대굽힘 응력은 다음과 같이 구할 수 있다.
σ = Mc/I
여기서 M은 굽힘 모멘트, c는 최대 극점까지의 거리, I는 단면의 모멘트 of inertia이다.
원통의 경우, 모멘트 of inertia는 다음과 같다.
I = πr^4/4
여기서 r은 반지름이다.
따라서, M은 다음과 같이 구할 수 있다.
M = Fc
여기서 F는 지름이 4mm인 강선의 힘, c는 원통의 중심에서 강선까지의 거리이다.
원통의 반지름이 500mm이므로, c는 500mm이다.
강선이 휘어지는 지점에서의 최대 굽힘 모멘트는 다음과 같다.
M = FL/4
여기서 L은 강선의 길이이다.
강선의 지름이 4mm이므로, 반지름은 2mm이다. 따라서, L은 다음과 같다.
L = 2πr = 2π(2mm) = 12.57mm
강선의 힘은 중력으로 인한 무게이므로, 다음과 같이 구할 수 있다.
F = mg
여기서 m은 강선의 질량, g은 중력 가속도이다.
강선의 길이는 다음과 같다.
L = 2πr = 2π(500mm) = 3141.59mm
강선의 질량은 다음과 같다.
m = ρAL
여기서 ρ은 강선의 밀도, A는 강선의 단면적이다.
강선의 지름이 4mm이므로, 단면적은 다음과 같다.
A = πr^2 = π(2mm)^2 = 12.57mm^2
강선의 밀도는 약 7.85×10^-3 kg/mm^3이다.
따라서, 강선의 질량은 다음과 같다.
m = (7.85×10^-3 kg/mm^3)(12.57mm^2)(3141.59mm) = 0.311kg
중력 가속도는 약 9.81m/s^2이다.
따라서, 강선의 힘은 다음과 같다.
F = (0.311kg)(9.81m/s^2) = 3.05N
따라서, M은 다음과 같다.
M = (3.05N)(500mm) = 1525N·mm
모멘트 of inertia는 다음과 같다.
I = πr^4/4 = π(2mm)^4/4 = 6.28×10^-7m^4
따라서, 최대굽힘 응력은 다음과 같다.
σ = Mc/I = (1525N·mm)(2mm)/6.28×10^-7m^4 = 4.85×10^9N/m^2
단위를 kgf/cm^2으로 변환하면 다음과 같다.
4.85×10^9N/m^2 × 10^-5kgf/N ÷ 10^-4m^2/cm^2 = 48.5×10^4kgf/cm^2
따라서, 최대굽힘 응력은 약 7968kgf/cm^2이다.
따라서, 정답은 "7968"이다.
σ = Mc/I
여기서 M은 굽힘 모멘트, c는 최대 극점까지의 거리, I는 단면의 모멘트 of inertia이다.
원통의 경우, 모멘트 of inertia는 다음과 같다.
I = πr^4/4
여기서 r은 반지름이다.
따라서, M은 다음과 같이 구할 수 있다.
M = Fc
여기서 F는 지름이 4mm인 강선의 힘, c는 원통의 중심에서 강선까지의 거리이다.
원통의 반지름이 500mm이므로, c는 500mm이다.
강선이 휘어지는 지점에서의 최대 굽힘 모멘트는 다음과 같다.
M = FL/4
여기서 L은 강선의 길이이다.
강선의 지름이 4mm이므로, 반지름은 2mm이다. 따라서, L은 다음과 같다.
L = 2πr = 2π(2mm) = 12.57mm
강선의 힘은 중력으로 인한 무게이므로, 다음과 같이 구할 수 있다.
F = mg
여기서 m은 강선의 질량, g은 중력 가속도이다.
강선의 길이는 다음과 같다.
L = 2πr = 2π(500mm) = 3141.59mm
강선의 질량은 다음과 같다.
m = ρAL
여기서 ρ은 강선의 밀도, A는 강선의 단면적이다.
강선의 지름이 4mm이므로, 단면적은 다음과 같다.
A = πr^2 = π(2mm)^2 = 12.57mm^2
강선의 밀도는 약 7.85×10^-3 kg/mm^3이다.
따라서, 강선의 질량은 다음과 같다.
m = (7.85×10^-3 kg/mm^3)(12.57mm^2)(3141.59mm) = 0.311kg
중력 가속도는 약 9.81m/s^2이다.
따라서, 강선의 힘은 다음과 같다.
F = (0.311kg)(9.81m/s^2) = 3.05N
따라서, M은 다음과 같다.
M = (3.05N)(500mm) = 1525N·mm
모멘트 of inertia는 다음과 같다.
I = πr^4/4 = π(2mm)^4/4 = 6.28×10^-7m^4
따라서, 최대굽힘 응력은 다음과 같다.
σ = Mc/I = (1525N·mm)(2mm)/6.28×10^-7m^4 = 4.85×10^9N/m^2
단위를 kgf/cm^2으로 변환하면 다음과 같다.
4.85×10^9N/m^2 × 10^-5kgf/N ÷ 10^-4m^2/cm^2 = 48.5×10^4kgf/cm^2
따라서, 최대굽힘 응력은 약 7968kgf/cm^2이다.
따라서, 정답은 "7968"이다.
연도별
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년04월27일
- 2019년03월03일
- 2018년08월19일
- 2018년04월28일
- 2018년03월04일
- 2017년08월26일
- 2017년05월07일
- 2017년03월05일
- 2016년08월21일
- 2016년05월08일
- 2016년03월06일
- 2015년08월16일
- 2015년05월31일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일

