2019년08월04일 60번
[전기자기학] 길이 ℓ(m)인 동축 원통 도체의 내외원통에 각각 +λ, -λ(C/m)의 전하가 분포되어 있다. 내외원통 사이의 유전율 ε인 유전체가 채워져 있을 때, 전계의 세기(V/m)는? (단, V는 내외원통 간의 전위차, D는 전속밀도이고, a, b는 내외원통의 반지름이며, 원통 중심에서의 거리 r은 a<r<b 인 경우이다.)
-
①
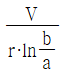
-
②
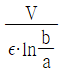
-
③
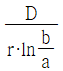
-
④
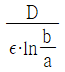
(정답률: 50%)
문제 해설




연도별
- 2021년08월14일
- 2020년08월22일
- 2019년08월04일
- 2018년08월19일
- 2016년08월21일
- 2016년03월06일
- 2015년08월16일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일
- 2011년08월21일
- 2011년06월12일
- 2011년03월20일
- 2008년07월27일
- 2008년05월11일
- 2008년03월02일
- 2006년08월03일
- 2005년05월29일
- 2004년08월08일
- 2004년05월23일
- 2004년03월07일
- 2003년08월10일
- 2003년05월25일
- 2003년03월16일
∮E·dA = Q/ε
여기서 Q는 내외원통 사이에 있는 전하의 총량이다. 내외원통에 있는 전하의 총량은 각각 λπaℓ, -λπbℓ이므로, Q = λπ(b^2 - a^2)ℓ이다.
내외원통의 대칭성을 이용하여 전기장의 방향이 반드시 원통의 축 방향과 일치하도록 가정할 수 있다. 이 경우, 가우스 법칙은 다음과 같이 쓸 수 있다.
EA - EB = Q/εA
여기서 EA, EB는 각각 내원통, 외원통의 표면에서의 전기장의 크기이다. 내원통과 외원통의 반지름을 각각 a, b라고 하면, EA = λa/εA, EB = -λb/εB이다.
따라서, 위의 식을 정리하면 다음과 같다.
E = λ/(2πεr)
여기서 r은 원통 중심에서의 거리이다. 따라서, 전계의 세기는 λ/(2πεr)이다.
정답은 "