2017년05월07일 8번

[실험계획법]
부적합품 여부에 대한 동일성에 관한 실험에서 적합품이면 0, 부적합품이면 1의 값을 주기로 하고 4대의 기계에서 나오는 200개씩의 제품에 대해서 부적합품 여부를 실험하여 그 결과로 아래와 같은 분산분석표를 구하였다. 다음 분산분석표의 일부자료를 이용하여 기계간의 부적합품률의 차에 관한 가설검정을 실시했을 때 판정기준으로 맞는 것은?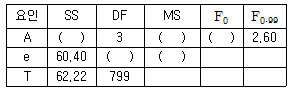

① F0＞F0.99(3, ve)이므로 기계간의 부적합품률의 차는 대단히 유의하다.
② F0＜F0.99(3, ve)이므로 기계간의 부적합품률의 차는 대단히 유의하다.
③ F0＞F0.99(ve, 3)이므로 기계간의 부적합품률의 차는 대단히 유의하다.
④ F0＜F0.99(ve, 3)이므로 기계간의 부적합품률의 차는 대단히 유의하다.

(정답률: 66%)

문제 해설

분산분석표에서 기계 간의 부적합품률의 차에 대한 가설검정을 실시하기 위해서는 "기계간의 제곱합(SS_A) / 기계간의 자유도(df_A)"와 "잔차제곱합(SS_E) / 잔차의 자유도(df_E)"를 이용하여 F-분포를 구해야 한다.

분산분석표에서 SS_A는 0.48, df_A는 3, SS_E는 2.52, df_E는 796으로 주어졌다.

이를 이용하여 F-분포를 구하면 F = (SS_A / df_A) / (SS_E / df_E) = (0.48 / 3) / (2.52 / 796) = 6.03이다.

이때, 유의수준 0.01에서의 F-분포의 임계값은 F_0.99 (3, 796) = 3.00이다.

따라서, F₀＞F_0.99 (3, 796)이므로 기계간의 부적합품률의 차는 대단히 유의하다는 것을 알 수 있다.

즉, 기계간의 부적합품률의 차가 우연에 의한 것이 아니라는 것을 유의수준 0.01에서 검증할 수 있다.

따라서, 정답은 "F₀＞F_0.99 (3, v_e)이므로 기계간의 부적합품률의 차는 대단히 유의하다."이다.

이전 문제 다음 문제

연도별

진행 상황

0 오답

0 정답