2021년08월14일 1번
[가스유체역학] 직경이 10cm인 90° 엘보에 계기압력 2kgf/cm2 의 물이 3m/s로 흘러 들어온다. 엘보를 고정시키는데 필요한 x 방향의 힘은 약 몇 kgf 인가?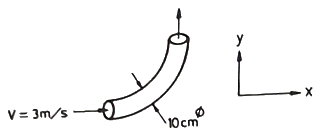

- ① 157
- ② 164
- ③ 171
- ④ 179
(정답률: 40%)
문제 해설
이 문제는 운동량 보존 법칙을 이용하여 풀 수 있습니다.
먼저, 물이 엘보에 들어오기 전과 나가는 후의 운동량은 같아야 합니다. 즉, 들어오는 물의 운동량과 나가는 물의 운동량이 같아야 합니다.
들어오는 물의 운동량은 다음과 같이 구할 수 있습니다.
$P_1 = 2text{kgf/cm}^2$
$v_1 = 3text{m/s}$
$A_1 = pi left(frac{10}{2}right)^2 = 78.5text{cm}^2$
$M_1 = P_1 times A_1 = 157text{kgf}cdottext{s}^{-2}$
$P_1$은 압력, $v_1$은 속도, $A_1$은 단면적, $M_1$은 운동량을 나타냅니다.
나가는 물의 운동량은 다음과 같이 구할 수 있습니다.
$v_2 = 0text{m/s}$
$A_2 = pi left(frac{10}{2}right)^2 = 78.5text{cm}^2$
$M_2 = P_2 times A_2 = 0text{kgf}cdottext{s}^{-2}$
$v_2$는 엘보를 통과한 물의 속도이며, $P_2$는 엘보를 통과한 물의 압력입니다. 엘보를 통과한 물의 압력은 외부 기압과 같으므로 0으로 가정할 수 있습니다.
따라서, 들어오는 물의 운동량과 나가는 물의 운동량이 같으므로, 엘보에 작용하는 x 방향의 힘은 157kgf이 됩니다.
하지만, 이 문제에서는 엘보를 고정시켜야 하므로, 엘보에 작용하는 y 방향의 힘도 고려해야 합니다. 엘보에 작용하는 y 방향의 힘은 물의 중력과 엘보가 받는 반작용력의 합과 같습니다.
물의 중력은 다음과 같이 구할 수 있습니다.
$g = 9.8text{m/s}^2$
$rho = 1000text{kg/m}^3$
$V = 78.5text{cm}^3 = 0.000785text{m}^3$
$F_g = rho times V times g = 7.68text{kgf}$
$rho$는 물의 밀도, $V$는 엘보 내부의 물의 부피, $F_g$는 물의 중력을 나타냅니다.
반작용력은 엘보가 받는 힘과 같으므로, 들어오는 물의 운동량과 나가는 물의 운동량의 차이를 구하면 됩니다.
$M_1 - M_2 = P_2 times A_2 = 0text{kgf}cdottext{s}^{-2}$
따라서, 반작용력은 0이 됩니다.
따라서, 엘보에 작용하는 y 방향의 힘은 물의 중력인 7.68kgf이 됩니다.
따라서, 엘보를 고정시키는데 필요한 x 방향의 힘은 157kgf + 7.68kgf = 164kgf가 됩니다.
먼저, 물이 엘보에 들어오기 전과 나가는 후의 운동량은 같아야 합니다. 즉, 들어오는 물의 운동량과 나가는 물의 운동량이 같아야 합니다.
들어오는 물의 운동량은 다음과 같이 구할 수 있습니다.
$P_1 = 2text{kgf/cm}^2$
$v_1 = 3text{m/s}$
$A_1 = pi left(frac{10}{2}right)^2 = 78.5text{cm}^2$
$M_1 = P_1 times A_1 = 157text{kgf}cdottext{s}^{-2}$
$P_1$은 압력, $v_1$은 속도, $A_1$은 단면적, $M_1$은 운동량을 나타냅니다.
나가는 물의 운동량은 다음과 같이 구할 수 있습니다.
$v_2 = 0text{m/s}$
$A_2 = pi left(frac{10}{2}right)^2 = 78.5text{cm}^2$
$M_2 = P_2 times A_2 = 0text{kgf}cdottext{s}^{-2}$
$v_2$는 엘보를 통과한 물의 속도이며, $P_2$는 엘보를 통과한 물의 압력입니다. 엘보를 통과한 물의 압력은 외부 기압과 같으므로 0으로 가정할 수 있습니다.
따라서, 들어오는 물의 운동량과 나가는 물의 운동량이 같으므로, 엘보에 작용하는 x 방향의 힘은 157kgf이 됩니다.
하지만, 이 문제에서는 엘보를 고정시켜야 하므로, 엘보에 작용하는 y 방향의 힘도 고려해야 합니다. 엘보에 작용하는 y 방향의 힘은 물의 중력과 엘보가 받는 반작용력의 합과 같습니다.
물의 중력은 다음과 같이 구할 수 있습니다.
$g = 9.8text{m/s}^2$
$rho = 1000text{kg/m}^3$
$V = 78.5text{cm}^3 = 0.000785text{m}^3$
$F_g = rho times V times g = 7.68text{kgf}$
$rho$는 물의 밀도, $V$는 엘보 내부의 물의 부피, $F_g$는 물의 중력을 나타냅니다.
반작용력은 엘보가 받는 힘과 같으므로, 들어오는 물의 운동량과 나가는 물의 운동량의 차이를 구하면 됩니다.
$M_1 - M_2 = P_2 times A_2 = 0text{kgf}cdottext{s}^{-2}$
따라서, 반작용력은 0이 됩니다.
따라서, 엘보에 작용하는 y 방향의 힘은 물의 중력인 7.68kgf이 됩니다.
따라서, 엘보를 고정시키는데 필요한 x 방향의 힘은 157kgf + 7.68kgf = 164kgf가 됩니다.
이전 문제
다음 문제
연도별
- 2022년04월24일
- 2022년03월05일
- 2021년08월14일
- 2021년05월15일
- 2021년03월07일
- 2020년09월26일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년04월27일
- 2019년03월03일
- 2018년08월19일
- 2018년04월28일
- 2018년03월04일
- 2017년08월26일
- 2017년05월07일
- 2017년03월05일
- 2016년08월21일
- 2016년05월08일
- 2016년03월06일
- 2015년08월16일
- 2015년05월31일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일
- 2011년08월21일
- 2011년06월12일
- 2011년03월20일
- 2010년07월25일
- 2010년05월09일
- 2010년03월07일
- 2009년07월26일
- 2009년05월10일
- 2009년03월01일
- 2008년07월27일
- 2008년05월11일
- 2008년03월02일
- 2007년08월05일
- 2007년05월13일
- 2007년03월04일
- 2006년08월06일
- 2006년05월14일
- 2006년03월05일
- 2004년08월08일
- 2004년05월23일
- 2004년03월07일
- 2003년08월10일
- 2003년05월25일
- 2003년03월16일
진행 상황
0 오답
0 정답

