2019년03월03일 12번
[일반기계공학] 그림과 같이 원형단면의 지름 d인 관성모멘트는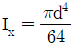 
이다. 원에 접하는 접선축에 대한 평행축의 정리를 활용하여 관성 모멘트(Ix)를 구하면?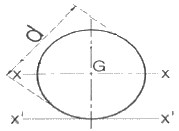
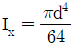이다. 원에 접하는 접선축에 대한 평행축의 정리를 활용하여 관성 모멘트(Ix)를 구하면?-
①
-
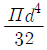
②
-
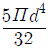
③
-
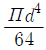
④
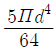
(정답률: 29%)
문제 해설
원형단면의 지름 d에 대한 관성모멘트는 Ix = (πd^4)/64 이다.
평행축의 정리에 따라, 원에 접하는 접선축에 대한 관성모멘트는 Ix = Iy + Ad^2/4 이다. 여기서 Iy는 원의 중심축에 대한 관성모멘트이고, A는 원의 면적이다.
원의 중심축에 대한 관성모멘트는 Iy = (πd^4)/64 이므로,
Ix = (πd^4)/64 + πd^2/4 x d^2/4
= (πd^4)/64 + (πd^4)/16
= (5πd^4)/64
따라서, 정답은 "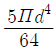" 이다.
이유는 평행축의 정리에 따라, 원에 접하는 접선축에 대한 관성모멘트는 중심축에 대한 관성모멘트와 면적에 대한 항이 더해진다는 것이다. 따라서, Ix는 원의 중심축에 대한 관성모멘트와 면적에 대한 항을 더한 값이다.
평행축의 정리에 따라, 원에 접하는 접선축에 대한 관성모멘트는 Ix = Iy + Ad^2/4 이다. 여기서 Iy는 원의 중심축에 대한 관성모멘트이고, A는 원의 면적이다.
원의 중심축에 대한 관성모멘트는 Iy = (πd^4)/64 이므로,
Ix = (πd^4)/64 + πd^2/4 x d^2/4
= (πd^4)/64 + (πd^4)/16
= (5πd^4)/64
따라서, 정답은 "
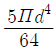" 이다. 이유는 평행축의 정리에 따라, 원에 접하는 접선축에 대한 관성모멘트는 중심축에 대한 관성모멘트와 면적에 대한 항이 더해진다는 것이다. 따라서, Ix는 원의 중심축에 대한 관성모멘트와 면적에 대한 항을 더한 값이다.
연도별
- 2022년04월24일
- 2022년03월05일
- 2021년08월14일
- 2021년05월15일
- 2021년03월07일
- 2020년09월26일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년04월27일
- 2019년03월03일
- 2018년08월19일
- 2018년04월28일
- 2018년03월04일
- 2017년08월26일
- 2017년05월07일
- 2017년03월05일
- 2016년08월21일
- 2016년05월08일
- 2016년03월06일
- 2015년08월16일
- 2015년05월31일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일
진행 상황
0 오답
0 정답