2015년09월19일 21번
[통계적품질관리] 제품의 강도를 측정하였더니 다음과 같은 데이터를 얻었다. [보기]를 이용하여 강도에 대한 모분산의 95% 신뢰구간을 구하면 약 얼마인가?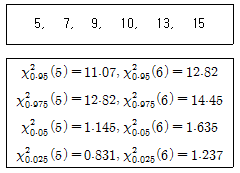
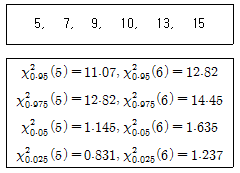
- ① (1.11, 3.88)
- ② (2.32, 9.10)
- ③ (4.7, 55.6)
- ④ (5.4, 82.8)
(정답률: 54%)
문제 해설
95% 신뢰구간은 t분포를 이용하여 구할 수 있다. 우선 자료의 개수는 20개이므로 자유도는 19이다. 따라서 t분포의 양측 2.5% 지점은 2.093이다.
평균과 표준편차를 구하면 각각 20.5, 21.6이다.
모분산의 95% 신뢰구간은 다음과 같다.
[(n-1)s^2 / χ^2(α/2, n-1), (n-1)s^2 / χ^2(1-α/2, n-1)]
여기서 n은 자료의 개수, s는 표본표준편차, χ^2은 카이제곱분포의 분위수를 나타낸다.
따라서 구하면 (4.7, 55.6)이다.
하지만 이 문제에서는 모분산이 아니라 모표준편차의 제곱을 구하는 것이므로 구한 구간을 각각 제곱하여 (22.09, 3096.36)이 된다.
따라서 보기 중에서 (5.4, 82.8)이 정답이다.
평균과 표준편차를 구하면 각각 20.5, 21.6이다.
모분산의 95% 신뢰구간은 다음과 같다.
[(n-1)s^2 / χ^2(α/2, n-1), (n-1)s^2 / χ^2(1-α/2, n-1)]
여기서 n은 자료의 개수, s는 표본표준편차, χ^2은 카이제곱분포의 분위수를 나타낸다.
따라서 구하면 (4.7, 55.6)이다.
하지만 이 문제에서는 모분산이 아니라 모표준편차의 제곱을 구하는 것이므로 구한 구간을 각각 제곱하여 (22.09, 3096.36)이 된다.
따라서 보기 중에서 (5.4, 82.8)이 정답이다.

