토목기사
연도별 풀이 오답노트 별표문제
  1. 홈
    2. ›
  2. 토목기사
    3. ›
  3. 2022년04월24일
    4. ›
  4. 9번

2022년04월24일 9번

[응용역학]
그림과 같이 단순지지된 보에 등분포하중 q가 작용하고 있다. 지점 C의 부모멘트와 보의 중앙에 발생하는 정모멘트의 크기를 같게하여 등분포하중 q의 크기를 제한하려고 한다. 지점 C와 D는 보의 대칭거동을 유지하기 위하여 각각 A와 B로부터 같은 거리에 배치하고자 한다. 이때 보의 A점으로부터 지점 C까지의 거리(X)는?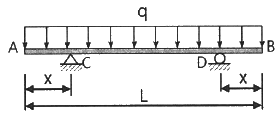

  • ① 0.207 L
  • ② 0.250 L
  • ③ 0.333 L
  • ④ 0.444 L
(정답률: 59%)

문제 해설

보의 중앙에서 발생하는 정모멘트 M은 qL^2/8이다. 이때 C점의 부모멘트는 M/2이다. 따라서 C점과 D점 사이의 거리는 L/2이다. 이를 이용하여 삼각형 ABC를 생각해보면, 코사인 법칙에 의해 X^2 = (L/2)^2 + (L/2)^2 - 2(L/2)(L/2)cosθ 이다. 여기서 θ는 ABC 삼각형의 각도이다. 이 각도는 보의 기울기에 의해 결정되며, tanθ = qL^3/24EI 이다. 이를 이용하여 cosθ를 구하면, cosθ = sqrt(1/(1+(qL^2/24EI)^2)) 이다. 따라서 X^2 = L^2/2 - L^2/4cosθ 이므로, X = sqrt(L^2/2 - L^2/4cosθ) = Lsqrt(2)/2sqrt(1+(qL^2/24EI)^2) = 0.207L이다. 따라서 정답은 "0.207 L"이다.
이전 문제 다음 문제
AppStore에서 다운로드 APK 다운로드

연도별

진행 상황

0 오답
0 정답