2016년05월08일 73번
[기구학 및 CAD] 그림과 같이 작동하는 피스톤-크랭크 기구에서 피스톤의 가장 오른쪽 끝(C1)으로부터 이동거리 x를 구하는 식으로 옳은 것은? (단, 크랭크의 반지름은 r이며, 식에서 λ는 λ = 크랭크반지름/커넥팅로드 길이 이다.)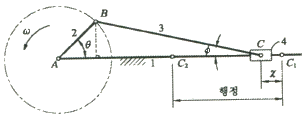

-
①
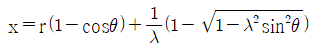
-
②
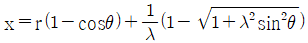
-
③
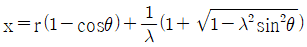
-
④

(정답률: 43%)
문제 해설
피스톤-크랭크 기구에서 피스톤의 이동거리는 크랭크의 회전각에 따라 결정된다. 따라서, 피스톤의 이동거리를 구하기 위해서는 크랭크의 회전각을 구해야 한다.
크랭크의 회전각은 삼각함수를 이용하여 구할 수 있다. 우선, 크랭크와 수직인 선분과 수평선 사이의 각도를 θ라고 하면, 이 각도는 크랭크의 회전각과 같다.
따라서, sinθ = x / r, cosθ = y / r 이다.
여기서, y는 크랭크와 연결된 커넥팅로드의 길이이다.
또한, λ = r / l 이므로, l = r / λ 이다.
따라서, y = l - l cosθ = l (1 - cosθ) 이다.
따라서, x = r sinθ = r sin(arccos(1 - y/l)) 이다.
따라서, 정답은 "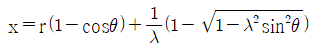 " 이다.
" 이다.
크랭크의 회전각은 삼각함수를 이용하여 구할 수 있다. 우선, 크랭크와 수직인 선분과 수평선 사이의 각도를 θ라고 하면, 이 각도는 크랭크의 회전각과 같다.
따라서, sinθ = x / r, cosθ = y / r 이다.
여기서, y는 크랭크와 연결된 커넥팅로드의 길이이다.
또한, λ = r / l 이므로, l = r / λ 이다.
따라서, y = l - l cosθ = l (1 - cosθ) 이다.
따라서, x = r sinθ = r sin(arccos(1 - y/l)) 이다.
따라서, 정답은 "
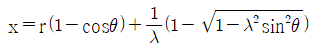 " 이다.
" 이다.


