2016년05월08일 74번
[기구학 및 CAD] 그림과 같이 4링크 회전 기구에서 순간 중심의 수는 몇 개인가?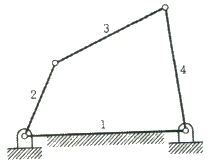

- ① 4
- ② 6
- ③ 8
- ④ 12
(정답률: 50%)
문제 해설
4링크 회전 기구에서는 각 링크가 다른 링크와 두 개의 관절로 연결되어 있으므로, 각 링크의 끝점은 다른 링크의 끝점을 중심으로 회전합니다. 따라서, 각 링크의 끝점이 중심이 될 수 있는 경우의 수를 모두 더하면 순간 중심의 수를 구할 수 있습니다.
1번 링크의 끝점은 2번 링크와 4번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
2번 링크의 끝점은 1번 링크와 3번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
3번 링크의 끝점은 2번 링크와 4번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
4번 링크의 끝점은 1번 링크와 3번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
따라서, 순간 중심의 수는 2+2+2+2=8개가 됩니다. 하지만, 이 중에서 중복되는 중심이 있으므로, 중복을 제거한 순간 중심의 수는 8/2=4개가 됩니다. 따라서, 정답은 "4"가 됩니다.
1번 링크의 끝점은 2번 링크와 4번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
2번 링크의 끝점은 1번 링크와 3번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
3번 링크의 끝점은 2번 링크와 4번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
4번 링크의 끝점은 1번 링크와 3번 링크의 끝점을 중심으로 회전할 수 있으므로, 2개의 중심이 될 수 있습니다.
따라서, 순간 중심의 수는 2+2+2+2=8개가 됩니다. 하지만, 이 중에서 중복되는 중심이 있으므로, 중복을 제거한 순간 중심의 수는 8/2=4개가 됩니다. 따라서, 정답은 "4"가 됩니다.



