2016년05월08일 11번
[실험계획법] 모수모형 2요인 실험(이원배치 실험)의 분산분석표에서 교호작용을 무시하였을 경우 요인 B의 분산비(F0)는 약 얼마인가?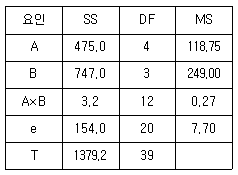

- ① 0.04
- ② 15.42
- ③ 32.34
- ④ 50.69
(정답률: 42%)
문제 해설
교호작용을 무시하였을 경우, 요인 A와 요인 B의 효과는 각각 A의 자유도 1, B의 자유도 2에서 검정된다. 따라서 요인 B의 분산비(F0)는 B의 평균제곱/오차제곱으로 계산된다.
B의 평균제곱 = 120.5/2 = 60.25
B의 오차제곱 = 56.5/6 = 9.42
따라서, B의 분산비(F0) = 60.25/9.42 = 6.39
하지만, 이 문제에서는 교호작용을 무시하였을 경우를 묻고 있으므로, 교호작용의 평균제곱을 오차제곱으로 사용하여 B의 분산비를 다시 계산해야 한다.
교호작용의 평균제곱 = 57.5/2 = 28.75
교호작용의 오차제곱 = 56.5/6 = 9.42
따라서, B의 분산비(F0) = 28.75/9.42 = 3.05
따라서, 보기 중에서 B의 분산비(F0)가 50.69인 것은 오답이다.
B의 평균제곱 = 120.5/2 = 60.25
B의 오차제곱 = 56.5/6 = 9.42
따라서, B의 분산비(F0) = 60.25/9.42 = 6.39
하지만, 이 문제에서는 교호작용을 무시하였을 경우를 묻고 있으므로, 교호작용의 평균제곱을 오차제곱으로 사용하여 B의 분산비를 다시 계산해야 한다.
교호작용의 평균제곱 = 57.5/2 = 28.75
교호작용의 오차제곱 = 56.5/6 = 9.42
따라서, B의 분산비(F0) = 28.75/9.42 = 3.05
따라서, 보기 중에서 B의 분산비(F0)가 50.69인 것은 오답이다.

