2016년05월08일 2번
[실험계획법] 모수요인(모수인자)인 온도의 3수준을 실험에서 고려하고자 한다. 온도의 각 수준은 실험자의 경험에 따라, 100, 120, 140℃로 고려하였다. i번째 수준에서 j번째 반복 실험 결과인 xij에 대해 다음과 같은 모형을 설정하였다. 모형의 가정으로 맞는 것은?

- ① a1+a2=-a3
- ② ai≥0
-
③

-
④
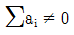
(정답률: 37%)
문제 해설
선형모형에서는 각 수준의 평균이 서로 다르다고 가정한다. 따라서 이 문제에서도 각 수준의 평균을 a1, a2, a3이라고 가정하고, 각 수준에서의 반응값은 해당 수준의 평균과 오차항으로 나눌 수 있다. 따라서 모형은 다음과 같다.
xij = ai + eij
여기서 eij는 오차항으로, 평균이 0이고 분산이 σ2인 정규분포를 따른다고 가정한다.
이제 모수요인이 3수준이므로, 각 수준에서의 평균을 추정하기 위해 3개의 식이 필요하다. 이를 위해 다음과 같은 제약조건을 설정한다.
a1 + a2 + a3 = 0
이는 각 수준의 평균이 서로 다르다는 가정에 따른 것으로, 모든 수준의 평균을 더하면 0이 되어야 한다는 것을 의미한다.
또한, 각 수준에서의 평균은 0 이상이므로 다음과 같은 제약조건도 설정한다.
ai ≥ 0 (i=1,2,3)
이제 이를 이용하여 모형을 다시 쓰면 다음과 같다.
xij = ai - (a1 + a2 + a3)/3 + eij
= ai - (a1 + a2)/3 - a3/3 + eij
따라서, a1 + a2 = -a3 이다.
xij = ai + eij
여기서 eij는 오차항으로, 평균이 0이고 분산이 σ2인 정규분포를 따른다고 가정한다.
이제 모수요인이 3수준이므로, 각 수준에서의 평균을 추정하기 위해 3개의 식이 필요하다. 이를 위해 다음과 같은 제약조건을 설정한다.
a1 + a2 + a3 = 0
이는 각 수준의 평균이 서로 다르다는 가정에 따른 것으로, 모든 수준의 평균을 더하면 0이 되어야 한다는 것을 의미한다.
또한, 각 수준에서의 평균은 0 이상이므로 다음과 같은 제약조건도 설정한다.
ai ≥ 0 (i=1,2,3)
이제 이를 이용하여 모형을 다시 쓰면 다음과 같다.
xij = ai - (a1 + a2 + a3)/3 + eij
= ai - (a1 + a2)/3 - a3/3 + eij
따라서, a1 + a2 = -a3 이다.

