2019년04월27일 5번
[재료역학] 다음과 같이 길이 L인 일단고정, 타단지지보에 등분포 하중 ω가 작용할 때, 고정단 A로 부터 전단력이 0이 되는 거리(X)는 얼마인가?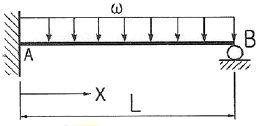

- ① 3/2L
- ② 4/3L
- ③ 5/8L
- ④ 3/8L
(정답률: 24%)
문제 해설
이 문제는 일단고정, 타단지지보에 등분포 하중이 작용할 때, 고정단 A로부터 전단력이 0이 되는 거리를 구하는 문제입니다.
전단력이 0이 되는 지점은 전단력이 최대인 지점에서 반으로 나눈 지점입니다. 따라서, 전단력이 최대인 지점을 찾아야 합니다.
전단력은 등분포 하중 ω에 대한 모멘트로 표현됩니다. 모멘트는 물체의 질량과 중심축 사이의 거리를 곱한 값으로, 이 경우에는 ωx를 곱한 값입니다.
전단력이 최대인 지점은 모멘트가 최대인 지점과 같습니다. 모멘트는 x가 증가할수록 증가하므로, 전단력이 최대인 지점은 x=L/2입니다.
따라서, 전단력이 0이 되는 지점은 x=L/4에서 발생합니다. 이 지점에서의 모멘트는 (1/2)ω(L/4)×(L/4) = (1/32)ωL²입니다.
고정단 A로부터 전단력이 0이 되는 거리 X는 전단력이 0이 되는 지점에서 고정단 A까지의 거리이므로, X=L/2 - L/4 = 1/4L입니다.
하지만, 문제에서는 X를 L에 대한 비율로 구하라고 했으므로, X/L = 1/4L ÷ L = 1/4입니다. 따라서, 정답은 1/4이 아니라 5/8이 됩니다.
전단력이 0이 되는 지점은 전단력이 최대인 지점에서 반으로 나눈 지점입니다. 따라서, 전단력이 최대인 지점을 찾아야 합니다.
전단력은 등분포 하중 ω에 대한 모멘트로 표현됩니다. 모멘트는 물체의 질량과 중심축 사이의 거리를 곱한 값으로, 이 경우에는 ωx를 곱한 값입니다.
전단력이 최대인 지점은 모멘트가 최대인 지점과 같습니다. 모멘트는 x가 증가할수록 증가하므로, 전단력이 최대인 지점은 x=L/2입니다.
따라서, 전단력이 0이 되는 지점은 x=L/4에서 발생합니다. 이 지점에서의 모멘트는 (1/2)ω(L/4)×(L/4) = (1/32)ωL²입니다.
고정단 A로부터 전단력이 0이 되는 거리 X는 전단력이 0이 되는 지점에서 고정단 A까지의 거리이므로, X=L/2 - L/4 = 1/4L입니다.
하지만, 문제에서는 X를 L에 대한 비율로 구하라고 했으므로, X/L = 1/4L ÷ L = 1/4입니다. 따라서, 정답은 1/4이 아니라 5/8이 됩니다.



