2012년08월26일 65번
[회로이론 및 제어공학] 다음 쌍곡선 함수의 라플라스 변환은?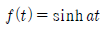
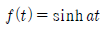
-
①

-
②

-
③
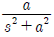
-
④
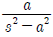
(정답률: 59%)
문제 해설
주어진 쌍곡선 함수는 지수함수의 합과 차로 이루어져 있으므로, 라플라스 변환의 선형성을 이용하여 각각의 항을 따로 계산할 수 있다.
먼저 첫 번째 항인 e^(-as) / (s-a)를 계산해보자. 이는 라플라스 변환의 정의에 따라 다음과 같이 계산할 수 있다.
L{e^(-as) / (s-a)} = ∫[0,∞] e^(-st) e^(-as) / (s-a) ds
= ∫[0,∞] e^(-(a+s)t) / (s-a) ds
= ∫[0,∞] e^(-ut) / u du (단, u=a+s)
= -ln(u) e^(-ut) |[0,∞]
= -ln(a+s) e^(-as)
다음으로 두 번째 항인 e^(as) / (s+a)를 계산해보자. 이 역시 라플라스 변환의 정의에 따라 다음과 같이 계산할 수 있다.
L{e^(as) / (s+a)} = ∫[0,∞] e^(-st) e^(as) / (s+a) ds
= ∫[0,∞] e^(-(s-a)t) / (s+a) ds
= ∫[0,∞] e^(-ut) / u du (단, u=s-a)
= -ln(u) e^(-ut) |[0,∞]
= -ln(s-a) e^(as)
따라서 전체 함수의 라플라스 변환은 위 두 항의 합으로 표현할 수 있으며, 이를 정리하면 다음과 같다.
L{(e^(-as) - e^(as)) / (s-a)(s+a)} = (-ln(a+s) + ln(s-a)) / (2a)
이때, 보기에서 정답으로 제시된 "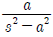 "는 위 식의 우변과 같으므로 정답이다.
"는 위 식의 우변과 같으므로 정답이다.
먼저 첫 번째 항인 e^(-as) / (s-a)를 계산해보자. 이는 라플라스 변환의 정의에 따라 다음과 같이 계산할 수 있다.
L{e^(-as) / (s-a)} = ∫[0,∞] e^(-st) e^(-as) / (s-a) ds
= ∫[0,∞] e^(-(a+s)t) / (s-a) ds
= ∫[0,∞] e^(-ut) / u du (단, u=a+s)
= -ln(u) e^(-ut) |[0,∞]
= -ln(a+s) e^(-as)
다음으로 두 번째 항인 e^(as) / (s+a)를 계산해보자. 이 역시 라플라스 변환의 정의에 따라 다음과 같이 계산할 수 있다.
L{e^(as) / (s+a)} = ∫[0,∞] e^(-st) e^(as) / (s+a) ds
= ∫[0,∞] e^(-(s-a)t) / (s+a) ds
= ∫[0,∞] e^(-ut) / u du (단, u=s-a)
= -ln(u) e^(-ut) |[0,∞]
= -ln(s-a) e^(as)
따라서 전체 함수의 라플라스 변환은 위 두 항의 합으로 표현할 수 있으며, 이를 정리하면 다음과 같다.
L{(e^(-as) - e^(as)) / (s-a)(s+a)} = (-ln(a+s) + ln(s-a)) / (2a)
이때, 보기에서 정답으로 제시된 "
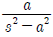 "는 위 식의 우변과 같으므로 정답이다.
"는 위 식의 우변과 같으므로 정답이다.



연도별
- 2022년04월24일
- 2022년03월05일
- 2021년08월14일
- 2021년05월15일
- 2021년03월07일
- 2020년09월26일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년04월27일
- 2019년03월03일
- 2018년08월19일
- 2018년04월28일
- 2018년03월04일
- 2017년08월26일
- 2017년05월07일
- 2017년03월05일
- 2016년08월21일
- 2016년05월08일
- 2016년03월06일
- 2015년08월16일
- 2015년05월31일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일
- 2011년08월21일
- 2011년06월12일
- 2011년03월20일
- 2010년07월25일
- 2010년05월09일
- 2010년03월07일
- 2009년07월26일
- 2009년05월10일
- 2009년03월01일
- 2008년07월27일
- 2008년05월11일
- 2008년03월02일
- 2007년08월05일
- 2007년05월13일
- 2007년03월04일
- 2006년08월06일
- 2006년05월14일
- 2006년03월05일
- 2005년08월07일
- 2005년05월29일
- 2005년03월06일
- 2004년08월08일
- 2004년05월23일
- 2004년03월07일
- 2003년08월10일
- 2003년05월25일
- 2003년03월16일
진행 상황
0 오답
0 정답