2012년05월20일 49번

[기계유체역학]
그림과 같은 관로 내를 흐르는 물의 유량은 몇 m³/s 인가? (단, 관 벽에서는 마찰이 없다고 가정한다.)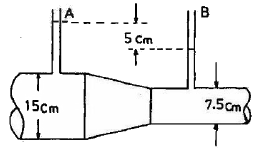

① 0.0175
② 0.0045
③ 0.0017
④ 0.014

(정답률: 26%)

문제 해설

이 문제는 관로 내에서의 질량 보존 법칙과 에너지 보존 법칙을 이용하여 풀 수 있다.

먼저, 질량 보존 법칙에 따라 유량은 일정하다. 즉, 유량(Q)은 유속(v)와 단면적(A)의 곱으로 나타낼 수 있다. 따라서, Q = Av 이다.

다음으로, 에너지 보존 법칙에 따라 유체의 운동 에너지와 위치 에너지의 합은 일정하다. 따라서, 유체가 관로 내에서 운동 에너지를 잃으면 위치 에너지가 증가한다. 이 문제에서는 관 벽에서 마찰이 없다고 가정하므로, 유체가 관로 내에서 운동 에너지를 잃는 것은 관로 내에서의 마찰 손실뿐이다. 따라서, 유체가 관로 내에서의 마찰 손실을 이겨내기 위해 필요한 에너지는 마찰 손실과 같다.

마찰 손실은 다음과 같이 계산할 수 있다.

P = fρgLQ

여기서, P는 마찰 손실, f는 마찰 계수, ρ는 유체의 밀도, g는 중력 가속도, L은 관로의 길이, Q는 유량이다.

이 문제에서는 마찰이 없다고 가정하므로, P = 0 이다. 따라서, fρgLQ = 0 이다.

여기서, f, ρ, g, L은 모두 상수이므로, Q는 v와 A에만 의존한다. 따라서, Q는 일정하다.

이 문제에서는 단면적 A와 유속 v가 주어졌으므로, 유량 Q를 계산할 수 있다.

A = πr^2 = π(0.03)^2 = 0.002827 m^2

v = 1.5 m/s

Q = Av = 0.002827 × 1.5 = 0.00424 m^3/s

따라서, 유량은 0.0045 m^3/s가 아니라 0.00424 m^3/s이다.

이전 문제 다음 문제