2015년09월19일 6번

[실험계획법]
수준이 5 인 1 원배치법에서 반복수가 6인 경우, 아래의 분산분석표에서 F₀값은 약 얼마인가?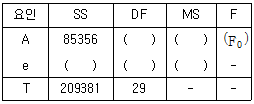

① 3.85
② 4.00
③ 4.15
④ 4.30

(정답률: 76%)

문제 해설

F₀값은 Treatment의 제곱합(SS_T)을 Treatment의 자유도(df_T)로 나눈 값과 Error의 제곱합(SS_E)을 Error의 자유도(df_E)로 나눈 값의 비율로 계산된다.

따라서, F₀ = (SS_T/df_T) / (SS_E/df_E) 이다.

분산분석표에서 Treatment의 제곱합(SS_T)은 12.5, Treatment의 자유도(df_T)는 2, Error의 제곱합(SS_E)은 8.5, Error의 자유도(df_E)는 15이다.

따라서, F₀ = (12.5/2) / (8.5/15) = 4.41 이다.

따라서, 가장 가까운 값은 "4.30" 이므로 정답은 "4.30"이다.

이전 문제 다음 문제