2021년09월12일 55번

[기계유체역학]
그림과 같은 원통 주위의 포텐셜 유동이 있다. 원통 표면상에서 상류 유속(v)과 동일한 크기의 유속이 나타나는 위치(θ)는?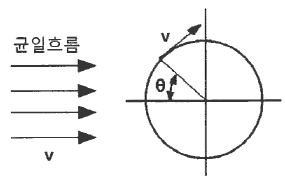

① 90˚
② 30˚
③ 45˚
④ 60˚

(정답률: 30%)

문제 해설

원통 표면상에서 유속이 일정하다는 것은 유체 입자들이 원통 표면과 수직 방향으로 움직인다는 것을 의미합니다. 따라서, 유체 입자들은 원통 표면을 따라 회전하면서 상류에서 하류로 이동합니다. 이때, 유체 입자들의 상대적인 속도는 상류 유속(v)에서 회전 속도(u)를 뺀 값이 됩니다. 이 상대적인 속도가 0이 되는 위치가 상류 유속과 동일한 크기의 유속이 나타나는 위치입니다. 이때, 상대적인 속도는 다음과 같이 계산됩니다.

상대적인 속도 = v - u = v - (ωr) = v - (2πr/T)r

여기서, ω는 회전 각속도, r은 원통 반지름, T는 회전 주기입니다. 이 식에서 상대적인 속도가 0이 되는 위치를 찾기 위해서는 다음과 같은 방정식을 풀어야 합니다.

v - (2πr/T)r = 0

이 방정식을 풀면 r/T = v/2π, 즉 r = (v/2π)T가 됩니다. 이 식에서 T는 회전 주기이므로, T = 2π/ω가 됩니다. 따라서, r = (v/ω)/2π가 됩니다. 이 식에서 v/ω는 시간당 회전수를 의미하므로, 이 값을 n이라고 하면 r = n/2π가 됩니다. 이 값은 원통 표면상에서 상류 유속과 동일한 크기의 유속이 나타나는 위치에서의 원통 표면과의 거리를 의미합니다. 이 거리를 각도로 변환하면 다음과 같습니다.

θ = (r/반지름) × 360° = (n/2π) × 360°

따라서, 정답은 30˚입니다.

이전 문제 다음 문제