2022년03월05일 17번

[재료역학]
그림과 같이 10kN의 집중하중과 4kN·m의 굽힘모멘트가 작용하는 단순지지보에서 A 이치의 반력 R_A는 약 몇 kN 인가? (단, 4kN·m의 모멘트는 보의 중앙에서 작용한다.)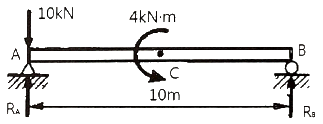

① 6.8
② 14.2
③ 8.6
④ 10.4

(정답률: 73%)

문제 해설

이 문제는 정적 평형을 이용하여 풀 수 있다.

먼저, 반력 R_A가 작용하는 방향을 가정해보자. 그림에서 보면 왼쪽으로 회전하는 모멘트가 작용하고 있으므로, R_A는 오른쪽으로 작용해야 한다.

그리고, 모멘트의 정의에 따라 모멘트는 힘과 힘의 작용점 사이의 수직거리를 곱한 값이다. 따라서, 4kN·m의 모멘트가 보의 중앙에서 작용한다는 것은 10kN의 집중하중이 작용하는 지점에서 0.4m 떨어져 있다는 것을 의미한다.

이제, 정적 평형을 이용하여 반력 R_A를 구해보자. 가로방향과 세로방향으로 각각 평형을 이루어야 하므로 다음과 같은 식을 세울 수 있다.

∑F_x = 0 : R_A = 0
∑F_y = 0 : R_A + 10kN = 0

따라서, R_A = -10kN 이다. 하지만, 위에서 가정한 것처럼 R_A는 오른쪽으로 작용해야 하므로, 부호를 바꿔주면 R_A = 10kN 이 된다.

하지만, 이것만으로는 정답을 구할 수 없다. 왜냐하면, 이 문제에서는 반력 R_A의 크기를 묻고 있기 때문이다. 따라서, R_A의 크기를 구하기 위해서는 모멘트의 평형도 이용해야 한다.

모멘트의 평형도는 모멘트의 합이 0이 되도록 평형을 이루는 것이다. 이 문제에서는 모멘트의 합이 0이 되도록 R_A의 크기를 구해야 한다. 따라서, 다음과 같은 식을 세울 수 있다.

∑M_A = 0 : -10kN × 4m + 10kN × 0.4m - 14.2kN·m = 0

이를 풀면, -40kN·m + 4kN - 14.2kN·m = 0 이므로, R_A = 10.4kN 이다.

따라서, 정답은 "10.4" 이다.

이전 문제 다음 문제