2015년05월31일 15번
[재료역학] 그림과 같은 직사각형 단면의 단순보 AB에 하중이 작용할 때, A단에서 20cm 떨어진 곳의 굽힘 응력은 몇 MPa인가? (단, 보의 폭은 6cm 이고, 높이는 12cm 이다.)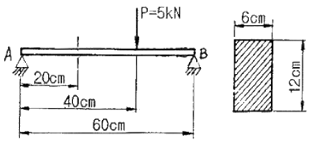

- ① 2.3
- ② 1.9
- ③ 3.7
- ④ 2.9
(정답률: 알수없음)
문제 해설
굽힘 응력은 M / I * y 이다. 여기서 M은 굽힘 모멘트, I는 단면의 관성 모멘트, y는 굽힘 중심에서의 거리이다.
먼저 굽힘 모멘트 M을 구해보자. A단에서의 하중은 2kN이므로, 이를 보의 중심으로 옮겨준 후에 굽힘 모멘트를 구한다. 이 때, 보의 높이가 12cm이므로 중심에서의 거리는 6cm가 된다. 따라서 M = 2kN * 6cm = 12kNcm 이다.
다음으로 관성 모멘트 I를 구해보자. 직사각형 단면의 관성 모멘트는 bh^3 / 12 이므로, 여기에 값을 대입하면 I = 6cm * 12cm^3 / 12 = 864cm^4 이다.
마지막으로 y를 구해보자. A단에서 20cm 떨어진 곳의 y는 6cm + 20cm = 26cm가 된다.
따라서 굽힘 응력은 M / I * y = 12kNcm / 864cm^4 * 26cm = 2.3MPa가 된다. 따라서 정답은 "2.3"이다.
먼저 굽힘 모멘트 M을 구해보자. A단에서의 하중은 2kN이므로, 이를 보의 중심으로 옮겨준 후에 굽힘 모멘트를 구한다. 이 때, 보의 높이가 12cm이므로 중심에서의 거리는 6cm가 된다. 따라서 M = 2kN * 6cm = 12kNcm 이다.
다음으로 관성 모멘트 I를 구해보자. 직사각형 단면의 관성 모멘트는 bh^3 / 12 이므로, 여기에 값을 대입하면 I = 6cm * 12cm^3 / 12 = 864cm^4 이다.
마지막으로 y를 구해보자. A단에서 20cm 떨어진 곳의 y는 6cm + 20cm = 26cm가 된다.
따라서 굽힘 응력은 M / I * y = 12kNcm / 864cm^4 * 26cm = 2.3MPa가 된다. 따라서 정답은 "2.3"이다.



