2011년03월20일 2번
[전기자기학] 자기 인덕턴스 L[H]인 코일에 전류 I[A]를 흘렸을 때, 자계의 세기가 H[AT/m]였다. 이 코일을 진공 중에서 자화시키는데 필요한 에너지 밀도[J/m3]는?
-
①
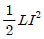
-
②
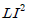
-
③
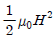
-
④
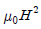
(정답률: 62%)
문제 해설
자기 인덕턴스 L은 다음과 같이 정의된다.
L = Φ/I
여기서 Φ는 자기 플럭스(자기장이 코일 내부를 통과하는 면적)이다. 따라서 Φ는 다음과 같이 구할 수 있다.
Φ = LI
자계의 세기 H는 다음과 같이 정의된다.
H = B/μ
여기서 B는 자기장의 밀도이고, μ는 자기적 계수이다. 진공 중에서 μ는 4π×10^-7이므로 다음과 같이 정리할 수 있다.
B = μH = 4π×10^-7H
자기 에너지 밀도는 다음과 같이 구할 수 있다.
w = (1/2)LI^2/V
여기서 V는 코일의 부피이다. 진공 중에서 V는 코일의 부피와 동일하므로 다음과 같이 정리할 수 있다.
w = (1/2)LI^2/V = (1/2)LI^2/(AL) = (1/2)I^2L/A
여기서 A는 코일의 면적이다. 따라서 w는 다음과 같이 구할 수 있다.
w = (1/2)I^2L/A = (1/2)I^2(Φ/I)/A = (1/2)ΦI/A
따라서 자기 에너지 밀도는 (1/2)ΦI/A이다. 이 값은 "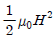 "이다. 이유는 코일의 자기 에너지는 자기 플럭스와 전류의 곱에 비례하며, 코일의 부피에 반비례하기 때문이다. 따라서 자기 에너지 밀도는 자기 플럭스와 전류의 곱에 비례하며, 코일의 면적에 반비례한다.
"이다. 이유는 코일의 자기 에너지는 자기 플럭스와 전류의 곱에 비례하며, 코일의 부피에 반비례하기 때문이다. 따라서 자기 에너지 밀도는 자기 플럭스와 전류의 곱에 비례하며, 코일의 면적에 반비례한다.
L = Φ/I
여기서 Φ는 자기 플럭스(자기장이 코일 내부를 통과하는 면적)이다. 따라서 Φ는 다음과 같이 구할 수 있다.
Φ = LI
자계의 세기 H는 다음과 같이 정의된다.
H = B/μ
여기서 B는 자기장의 밀도이고, μ는 자기적 계수이다. 진공 중에서 μ는 4π×10^-7이므로 다음과 같이 정리할 수 있다.
B = μH = 4π×10^-7H
자기 에너지 밀도는 다음과 같이 구할 수 있다.
w = (1/2)LI^2/V
여기서 V는 코일의 부피이다. 진공 중에서 V는 코일의 부피와 동일하므로 다음과 같이 정리할 수 있다.
w = (1/2)LI^2/V = (1/2)LI^2/(AL) = (1/2)I^2L/A
여기서 A는 코일의 면적이다. 따라서 w는 다음과 같이 구할 수 있다.
w = (1/2)I^2L/A = (1/2)I^2(Φ/I)/A = (1/2)ΦI/A
따라서 자기 에너지 밀도는 (1/2)ΦI/A이다. 이 값은 "
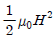 "이다. 이유는 코일의 자기 에너지는 자기 플럭스와 전류의 곱에 비례하며, 코일의 부피에 반비례하기 때문이다. 따라서 자기 에너지 밀도는 자기 플럭스와 전류의 곱에 비례하며, 코일의 면적에 반비례한다.
"이다. 이유는 코일의 자기 에너지는 자기 플럭스와 전류의 곱에 비례하며, 코일의 부피에 반비례하기 때문이다. 따라서 자기 에너지 밀도는 자기 플럭스와 전류의 곱에 비례하며, 코일의 면적에 반비례한다.



연도별
- 2022년04월24일
- 2022년03월05일
- 2021년08월14일
- 2021년05월15일
- 2021년03월07일
- 2020년09월26일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년04월27일
- 2019년03월03일
- 2018년08월19일
- 2018년04월28일
- 2018년03월04일
- 2017년08월26일
- 2017년05월07일
- 2017년03월05일
- 2016년08월21일
- 2016년05월08일
- 2016년03월06일
- 2015년08월16일
- 2015년05월31일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년05월20일
- 2012년03월04일
- 2011년08월21일
- 2011년06월12일
- 2011년03월20일
- 2010년07월25일
- 2010년05월09일
- 2010년03월07일
- 2009년07월26일
- 2009년05월10일
- 2009년03월01일
- 2008년07월27일
- 2008년05월11일
- 2008년03월02일
- 2007년08월05일
- 2007년05월13일
- 2007년03월04일
- 2006년08월06일
- 2006년05월14일
- 2006년03월05일
- 2005년08월07일
- 2005년05월29일
- 2005년03월06일
- 2004년08월08일
- 2004년05월23일
- 2004년03월07일
- 2003년08월10일
- 2003년05월25일
- 2003년03월16일
진행 상황
0 오답
0 정답