2008년05월11일 69번

[회로이론 및 제어공학]
RC 저역 여파기 회로의 전달함수 G(jω)에서 ω=1/(RC)인 경우 |G(jω)|의 값은?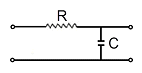

① 1
② 0.707
③ 0.5
④ 0

(정답률: 49%)

문제 해설

전달함수 G(jω)는 다음과 같이 표현할 수 있다.

G(jω) = 1 / (1 + jωRC)

여기서 ω=1/(RC)인 경우를 생각해보자.

G(jω=1/(RC)) = 1 / (1 + j)

이를 복소수 평면 상에서 표현하면 다음과 같다.

여기서 |G(jω)|의 값은 복소수 평면 상에서 원점(0,0)에서 G(jω)의 위치까지의 거리를 나타내는 크기이다. 따라서 위 그림에서 원점과 G(jω)의 거리를 구하면 |G(jω)|의 값이 된다.

원점과 G(jω)의 거리를 구하기 위해서는 피타고라스의 정리를 이용할 수 있다.

|G(jω)| = √(1² + 1²) / 2 = 0.707

따라서 정답은 "0.707"이다. 이 값은 RC 저역 여파기 회로에서 입력 신호의 진폭을 1/√2로 감소시키는 역할을 한다. 이를 "저역통과 필터"라고도 부른다.

이전 문제 다음 문제